Imagine a world where intricate electronic circuits – the very foundation of our modern technology – could be simplified, made more efficient, and even cheaper to produce. This is the promise of Boolean algebra, a powerful mathematical tool that allows us to unravel the complex logic behind circuits and optimize their design. This article delves into the fascinating world of Boolean algebra, exploring the fundamental concepts and practical applications that make it a cornerstone of electrical engineering and computer science.
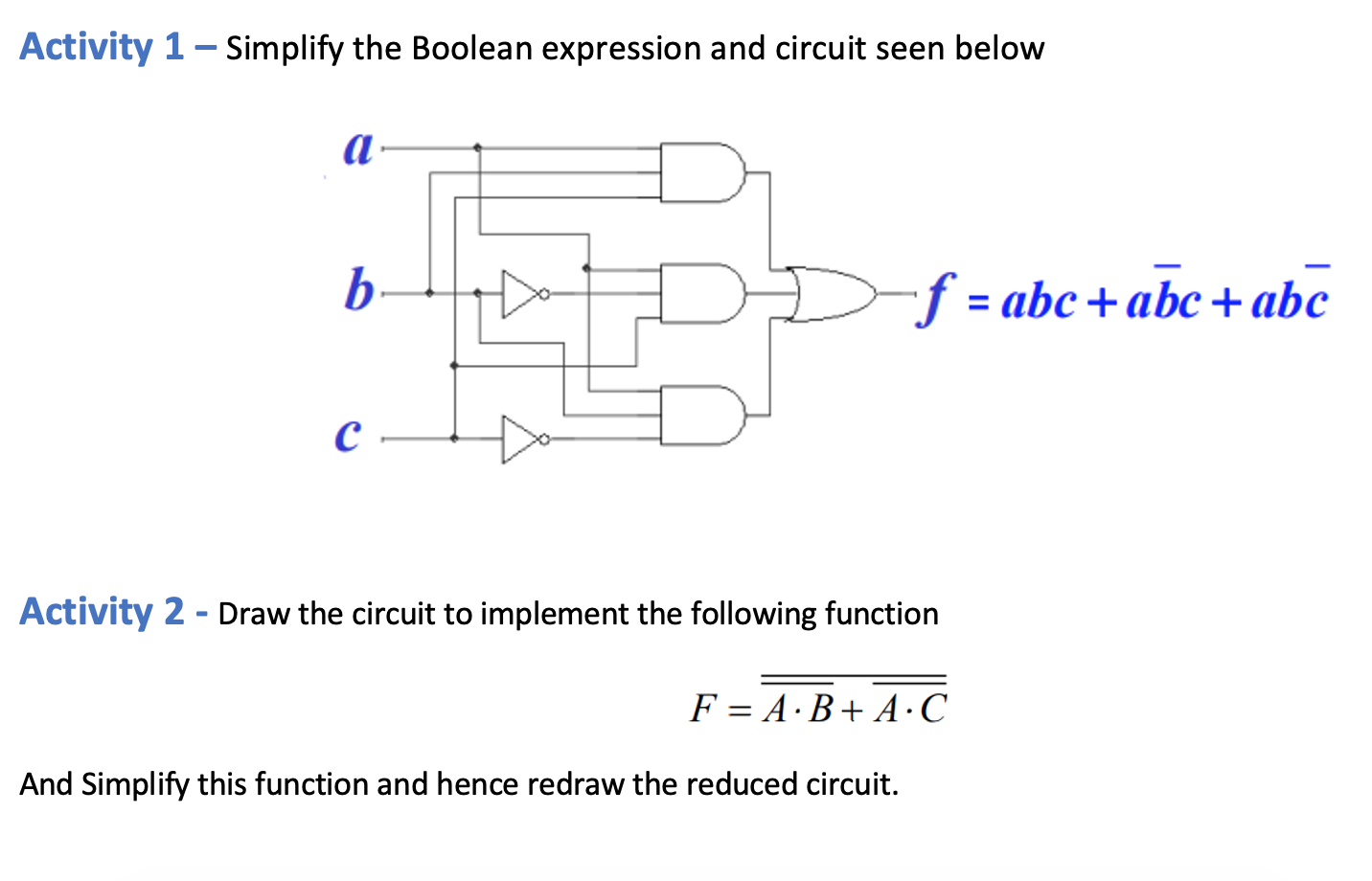
Image: www.chegg.com
Activity 2.1.4, often found in introductory electronics courses, guides us through the process of circuit simplification using Boolean algebra. This process is not just about reducing the number of components in a circuit; it’s about optimizing performance, minimizing cost, and ensuring error-free operation. Even if you’re not an aspiring electrical engineer, understanding the principles of Boolean algebra offers a fascinating glimpse into the inner workings of the digital devices that permeate our daily lives.
A Gateway to Logical Thinking: Demystifying Boolean Algebra
At its core, Boolean algebra operates on a system of logic, dealing with “true” or “false” values. These values are represented by 1 and 0, respectively, which you might recognize as the binary digits used in computer processing. Just as basic arithmetic deals with numbers and operations like addition and subtraction, Boolean algebra focuses on logical operations like “AND”, “OR”, and “NOT”.
- AND: The AND operation is true only if both inputs are true. Imagine a simple switch controlling a light. It will turn on only if both the switch and the power supply are active. In Boolean notation, this is represented as A AND B = 1, only if both A = 1 and B = 1.
- OR: The OR operation is true if at least one of the inputs is true. Think of a door with two separate activation mechanisms – a button and a weight sensor. The door will open if either the button is pressed or someone steps on the sensor. In Boolean terms, this is A OR B = 1 if either A = 1 or B = 1 (or both are 1).
- NOT: The NOT operation inverts the input. If a signal is “true” (1), the NOT operation makes it “false” (0), and vice versa. Picture a light switch with a toggle. The light is on when the switch is in one position and off when it’s in the other. This “flip-flopping” behavior is mirrored by the NOT operation.
Circuit Simplification: Unraveling the Complex with Boolean Algebra
Let’s delve deeper into circuit simplification and explore how Boolean algebra provides the roadmap. Imagine a complex circuit with numerous gates (AND, OR, NOT) and interconnected wires. This circuit, even if it performs its intended function, might be inefficient, bulky, and prone to errors.
This is where Boolean algebra steps in. By representing the circuit using Boolean expressions, we can apply simplification laws—similar to the rules you learned in algebra—to reduce the complexity. Here are a few key laws:
- Commutative Law: A AND B = B AND A and A OR B = B OR A. The order of the inputs doesn’t matter in AND and OR operations.
- Associative Law: (A AND B) AND C = A AND (B AND C) and (A OR B) OR C = A OR (B OR C). We can group the variables without altering the outcome in AND and OR operations.
- Distributive Law: A AND (B OR C) = (A AND B) OR (A AND C) and A OR (B AND C) = (A OR B) AND (A OR C). This law is often used to expand or factorize expressions.
- Identity Law: A AND 1 = A and A OR 0 = A. The identity element in AND is 1, and in OR it’s 0.
- Complement Law: A AND (NOT A) = 0 and A OR (NOT A) = 1. Combining a variable with its inverse using AND results in 0, while combining them with OR results in 1.
By recognizing these laws and applying them strategically, we can simplify Boolean expressions, resulting in circuits with fewer components, improved performance, and reduced cost.
Activity 2.1.4: A Practical Guide to Circuit Simplification
Activity 2.1.4, a common activity in introductory electronics courses, provides a hands-on approach to applying Boolean algebra principles. Here’s a typical example:
- Develop a Circuit: Start with a circuit diagram, using standard symbols for gates like AND (represented by a gate with an output and two inputs labeled ‘A’ and ‘B’).
- Create the Boolean Expression: Represent this circuit using Boolean expressions based on the logic gates and inputs. For example, if the circuit has two AND gates with outputs ‘C’ and ‘D’, followed by an OR gate with output ‘E’, you’d have an expression like E = (A AND B) OR (C AND D).
- Apply Simplification Laws: Now, use the Boolean algebra laws to simplify the expression. You might find opportunities to combine terms, eliminate redundancies, or factor out common elements.
- Redesign the Circuit: Finally, translate the simplified expression back into a circuit diagram, using fewer components.
By working through these steps, students gain a practical understanding of how Boolean algebra can be used to optimize circuit designs.
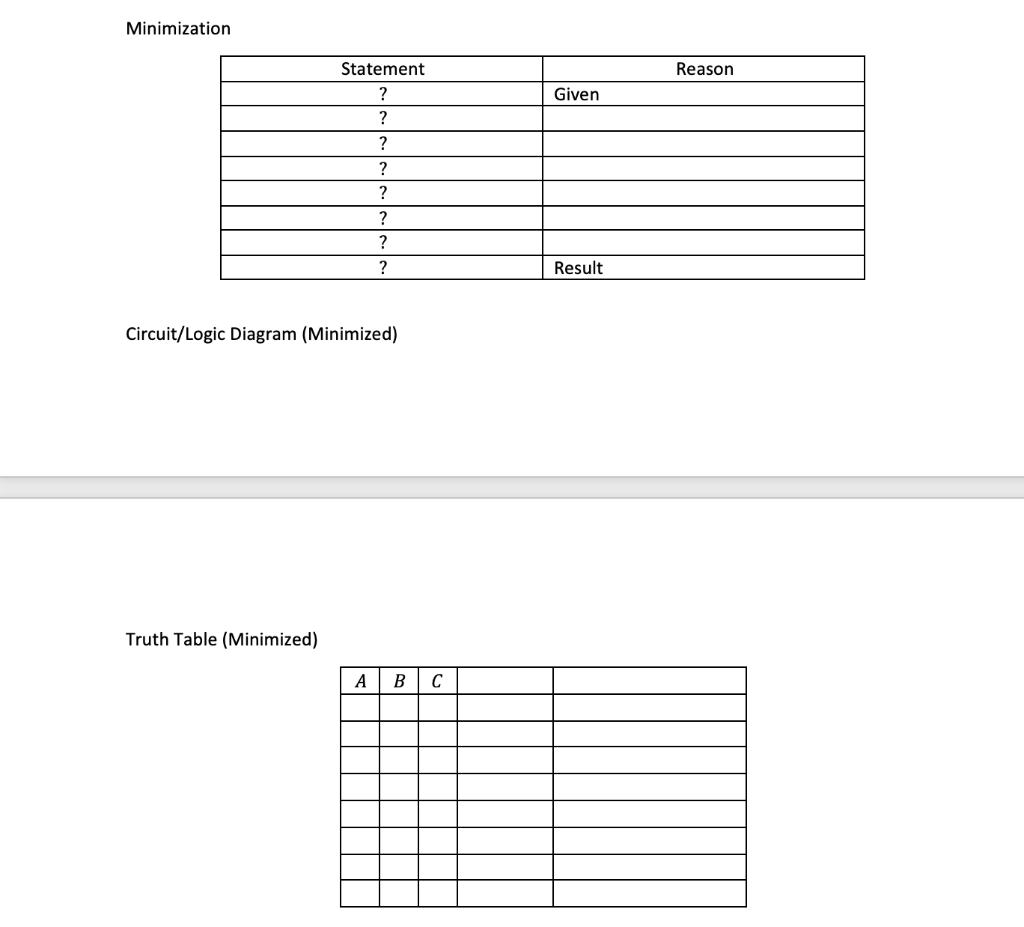
Image: www.chegg.com
Beyond the Textbook: Real-World Applications of Boolean Algebra
While activity 2.1.4 focuses on the fundamentals, the applications of Boolean algebra extend far beyond textbook examples. They are the lifeblood of modern technology, shaping the world around us:
- Digital Logic Design: Boolean algebra is the foundation of digital logic circuits, the building blocks of computers, smartphones, and other digital devices. From CPU design to memory systems, Boolean logic ensures the faithful processing and storage of information.
- Computer Programming: Many programming languages use logical operators (AND, OR, NOT) that are rooted in Boolean algebra. Programmers leverage these operators to construct complex decision-making structures within their programs.
- Database Management: Boolean operators are essential for database queries, allowing users to filter data according to specific criteria. You use these operators every time you search for information online or refine a list of items based on certain properties.
- Artificial Intelligence: Boolean logic is applied in AI systems for pattern recognition, expert systems, and decision trees. It helps machines make logical deductions and inferences based on input data.
Expert Tips for Mastering Boolean Algebra
To truly grasp the power of Boolean algebra, consider these expert tips from seasoned engineers and educators:
- Practice Makes Perfect: Just like learning a musical instrument or a new language, mastery of Boolean algebra comes with practice. Work through numerous examples, solve problems, and design your circuits.
- Visualize the Logic: Instead of just memorizing symbols and equations, try to visualize the logic underlying each Boolean operation. Imagine gates as physical switches, and think about how the relationships between them affect the flow of signals.
- Embrace Tools and Resources: Don’t hesitate to use software tools designed for Boolean algebra simplification. These tools can streamline the process and provide valuable insights. Explore resources like online tutorials, videos, or textbooks to deepen your understanding.
Activity 2.1 4 Circuit Simplification Boolean Algebra
Looking Ahead: The Future of Boolean Algebra
As technology continues to advance at an unprecedented pace, Boolean algebra remains a vital tool for designing and optimizing complex digital systems. The future holds exciting developments in areas like quantum computing, where Boolean logic is being explored to develop new computational paradigms.
Whether you’re an aspiring engineer, a tech enthusiast, or simply curious about the workings of the digital world, understanding Boolean algebra empowers you to appreciate the elegance and efficiency hidden within the circuits that power our lives.
So, go forth, explore the world of Boolean logic, and unlock the secrets of digital innovation.





