Have you ever looked at a circle and felt a sense of awe at its perfect, continuous form? Circles are everywhere, from the wheel that revolutionized transportation to the orbits of planets in the vastness of space. They hold a mathematical elegance that has fascinated scholars for centuries. But what about the theorems that govern these seemingly simple shapes? Prepare to delve into a world of angles, chords, and tangents as we explore the incredible power of circle theorems.
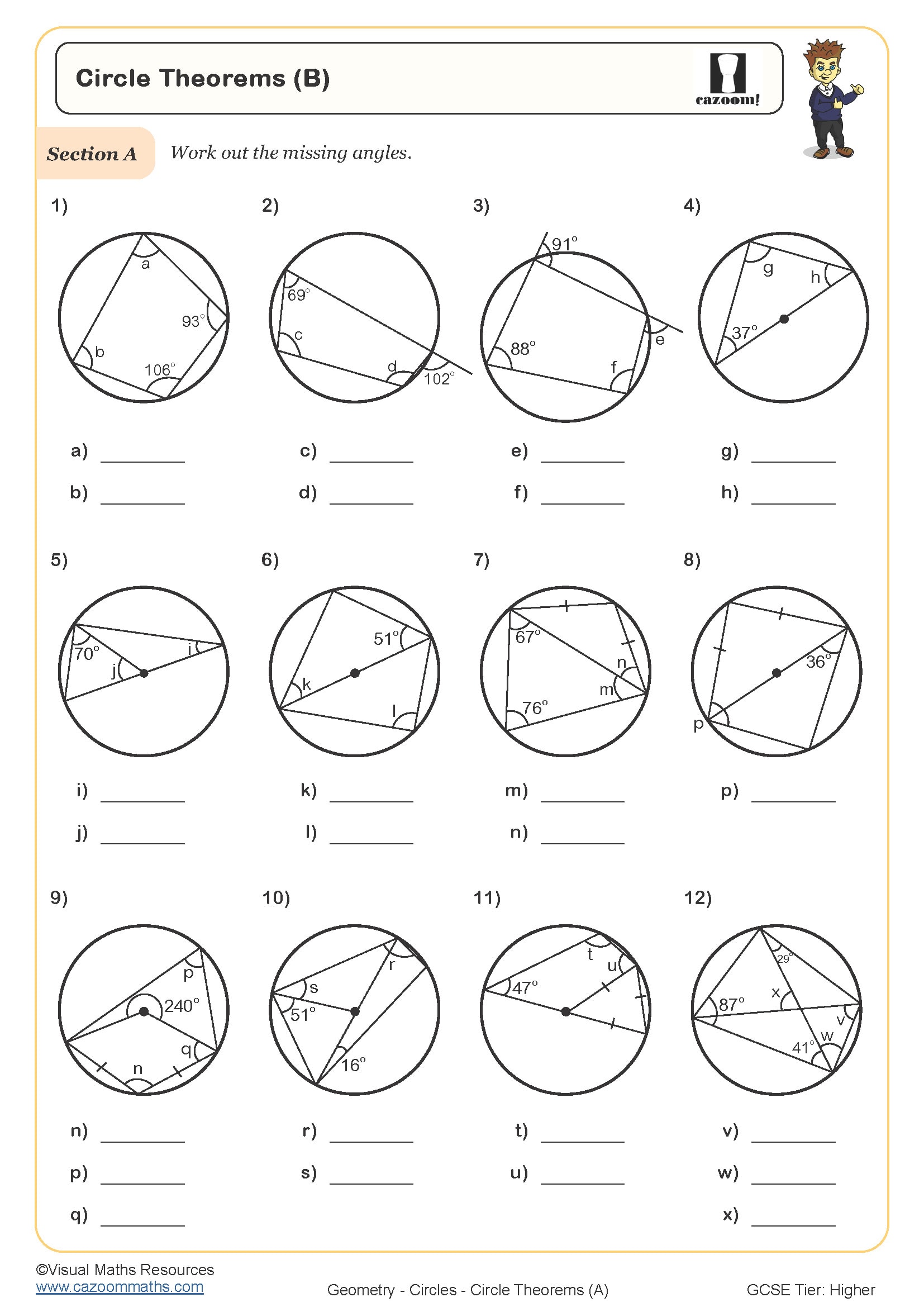
Image: worksheets.ekocraft-appleleaf.com
Today, we are going to unravel the mysteries of circle theorems and show you how to tackle those tricky questions with confidence. Whether you are a student grappling with geometry homework or an adult looking to refresh your math skills, this guide will equip you with the knowledge and resources you need to master circle theorems.
The Beauty of Circle Theorems: A Foundation of Geometry
Circle theorems are a set of rules that describe the relationships between lines, angles, and arcs within a circle. They provide a framework for understanding the geometry of circles and solving a wide range of problems. These theorems are not merely abstract concepts; they are the foundation for many real-world applications, from designing bridges and buildings to understanding the path of light and sound waves.
Essential Theorems – Your Toolkit for Circle Geometry
To navigate the world of circle theorems, you need to understand the core concepts. Imagine a circle as a canvas where lines and angles dance according to specific rules. Let’s start by exploring some of the essential theorems that form the basis of this dance:
-
Central Angle Theorem: The central angle, formed by two radii, is twice the measure of any inscribed angle that intercepts the same arc. Imagine a pie slice – the central angle is the angle at the center, and the inscribed angle is the angle captured at the edge of the pie crust.
-
Inscribed Angle Theorem: Any inscribed angle that intercepts a specific arc has a measure that is half the measure of the central angle intercepting the same arc. Think of it like looking at a pie from the side – the inscribed angle is the angle you see, and the central angle is the angle at the center.
-
Tangent-Chord Theorem: The angle formed by a tangent line and a chord at the point of tangency is equal to half the measure of the intercepted arc. Imagine a pencil touching a circle – the angle between the pencil and the circle’s edge is half the angle of the arc intercepted by the pencil.
-
Intersecting Chords Theorem: When two chords intersect inside a circle, the product of the segments of one chord is equal to the product of the segments of the other chord. Think of it like a puzzle – the pieces (segments) interlock in a precise way.
-
Tangents from an External Point: When two tangent lines are drawn from an external point to a circle, the segments of the tangent lines are congruent, and the angle formed by the tangent lines is bisected by the line connecting the external point to the center of the circle. Imagine a spiderweb – the threads (tangents) from an outside point are equal, and the angle between them is perfectly split.
Navigating the Labyrinth of Circle Theorem Problems
Armed with these key theorems, let’s tackle some common types of circle theorem problems. These problems typically ask you to calculate the measure of angles, arcs, or segments within a circle. Don’t be intimidated! With practice and a logical approach, you’ll master these challenges. Here’s a breakdown of typical problems:
-
Calculating Angles: You’ll be given a diagram with a circle and asked to find the measure of an angle. Identify the key elements: central angles, inscribed angles, tangent lines, and chords. Apply the relevant theorems to find the angle.
-
Determining Arc Lengths: Similar to angle problems, but you’ll be asked to find the length of a specific arc. Recall the relationship between angles and arcs, and utilize the relevant theorem to calculate the arc length.
-
Finding Segment Lengths: These problems involve finding the lengths of chords, tangents, or segments formed by intersecting lines within a circle. Remember the theorems related to chords, tangents, and their intersections.

Image: www.pinterest.com.au
Mastering Circle Theorems: Practice Makes Perfect
The best way to become a circle theorem champion is through practice. Numerous resources are available to help you hone your skills:
-
Textbooks: Explore textbooks on geometry to find detailed explanations and practice problems.
-
Online Resources: Utilize websites dedicated to math, such as Khan Academy, for interactive resources, tutorials, and practice quizzes.
-
PDFs: Many websites offer free PDFs containing circle theorem questions and answers. Use these resources to test your understanding and identify areas where you need more practice.
-
Practice Problems: Seek out practice problems aligned with your learning level. Start with simple examples and gradually increase the difficulty.
Unlocking the Potential of Circle Theorems: Beyond the Textbook
Circle theorems are more than just classroom concepts. They underpin a remarkable array of real-world applications, proving their practical relevance beyond the confines of textbooks:
-
Architecture: Architects use circle theorems to design structures like domes and arches, ensuring stability and optimizing space. Think of the Pantheon in Rome – its dome is a testament to the power of circle geometry.
-
Engineering: Engineers rely on circle theorems to design bridges, tunnels, and other infrastructure, ensuring efficient load distribution and optimal structural integrity.
-
Physics: Circle theorems play a critical role in understanding wave phenomena, such as circular waves created by a pebble dropped in water.
-
Astronomy: Astronomers use circle theorems to calculate distances and orbits of celestial objects, unraveling the mysteries of the cosmos.
Circle Theorem Questions And Answers Pdf
Empowering Yourself with Knowledge: A Journey of Discovery
Circle theorems offer more than just problem-solving skills. They open doors to a deeper understanding of geometry and provide valuable insights into real-world applications. The journey of mastering circle theorems may seem daunting at first, but with dedication and a willingness to explore, you’ll unlock a world of knowledge and find yourself confidently tackling problems that once seemed impossible.
Remember, the most important aspect is the journey itself – embrace the challenges, celebrate your successes, and enjoy the satisfaction of unraveling the secrets of the circle.





