Have you ever wondered how your smartphone or computer calculates the result of 2 + 2, or performs more complex operations like multiplying two large numbers? The answer lies in the fascinating world of digital logic, where simple gates like XOR and XNOR, along with the ingenious design of binary adders, form the foundation of modern computing.
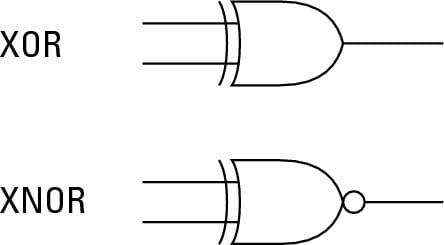
Image: www.176iot.com
This article delves into the intricate workings of XOR and XNOR gates, exploring their role in binary arithmetic and their crucial contribution to the operation of binary adders. By understanding these foundational concepts, you’ll gain a deeper appreciation for the elegant simplicity that underpins the incredible power of modern computers.
Understanding XOR and XNOR Gates
XOR: The Exclusive OR Gate
The XOR (Exclusive OR) gate is a fundamental logic gate in digital electronics. It produces a true (1) output only when its two inputs are different. If both inputs are the same (either both 0 or both 1), the output is false (0). You can visualize its operation using a truth table:
| Input A | Input B | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The XOR gate is crucial in numerous digital applications, including:
- Parity Checking: Used in data transmission to detect errors by ensuring the number of 1s in a data packet is even or odd.
- Data Encryption: Employed in cryptographic algorithms to perform bitwise operations and protect sensitive information.
- Control Circuits: Used in digital circuits to control the flow of data and the execution of tasks.
XNOR: The Exclusive NOR Gate
The XNOR (Exclusive NOR) gate is the antithesis of the XOR gate. It produces a true (1) output when its two inputs are the same (both 0 or both 1), and a false (0) output when they are different. Just like XOR, its operation can be represented in a truth table:
| Input A | Input B | Output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
The XNOR gate plays a vital role in:
- Equality Comparisons: Used in digital circuits to compare two binary values for equality.
- Data Selection: Used in multiplexers, which select data from different sources based on a control signal.
- Combinational Logic: Used in complex digital circuits to implement specific logic functions.

Image: joeeagle.weebly.com
The Foundation of Binary Arithmetic: Binary Adders
Binary adders are the workhorses of binary arithmetic, capable of adding two binary numbers digit by digit. They rely on the XOR and XNOR gates, along with other fundamental logic gates, to perform their calculations efficiently. Let’s explore the construction and operation of a simple half-adder, the building block of more complex binary adders.
The Half-Adder: Adding Two Bits
A half-adder is a basic digital circuit that can add two single-bit binary numbers (0 or 1). It consists of an XOR gate to generate the sum (S) and an AND gate to generate the carry-out (C).
- Sum (S): The XOR gate produces the sum bit, which is 1 if one of the inputs is 1, and 0 if both are 0 or both are 1.
- Carry-out (C): The AND gate produces the carry-out bit, which is 1 only if both inputs are 1.
Here’s the truth table for a half-adder:
| Input A | Input B | Sum (S) | Carry-out (C) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
As you can see, the half-adder correctly adds two single-bit binary numbers:
- 0 + 0 = 0 (sum=0, carry=0)
- 0 + 1 = 1 (sum=1, carry=0)
- 1 + 0 = 1 (sum=1, carry=0)
- 1 + 1 = 0 (sum=0, carry=1)
The Full-Adder: Adding with Carry
While a half-adder can add two single-bit numbers, it cannot handle carry-in bits. This is where the full-adder comes into play. A full-adder is a digital circuit designed to add three single-bit binary numbers: two input bits (A and B) and a carry-in bit (Cin). It produces two outputs: a sum bit (S) and a carry-out bit (Cout).
The full-adder typically uses two half-adders and an OR gate. The first half-adder adds the two input bits (A and B), producing a sum bit (S1) and a carry-out bit (C1). The second half-adder adds the carry-in bit (Cin) to the sum bit from the first half-adder (S1), generating the final sum bit (S) and a second carry-out bit (C2). Finally, the OR gate combines the two carry-out bits (C1 and C2) to produce the final carry-out (Cout).
The truth table for a full-adder is more complex than that of a half-adder, reflecting the addition of three bits:
| Input A | Input B | Carry-in (Cin) | Sum (S) | Carry-out (Cout) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
The full-adder is essential for adding multi-bit binary numbers, forming the building block for the ripple-carry adder discussed next.
Adding Multi-Bit Numbers: The Ripple-Carry Adder
To add multi-bit binary numbers, we use a ripple-carry adder, which is a chain of full-adders. Each full-adder takes two corresponding bits from the input numbers and the carry-out from the previous full-adder as inputs. The result is a sum bit and a carry-out bit, which is passed to the next full-adder in the chain. This process “ripples” the carry from one full-adder to the next, hence the name “ripple-carry adder.”
For example, to add two 4-bit numbers (1011 and 0110), you would use four full-adders connected in series. Each full-adder adds a corresponding pair of bits from the input numbers and the previous carry-out (the first full-adder would receive a carry-in of 0). The resulting sum bits from each full-adder form the final sum (10001), while the carry-out from the last full-adder (1) indicates a “carry-out” from the most significant bit.
Ripple-carry adders are relatively simple to implement and are commonly used in basic digital circuits. However, as the number of bits increases, the delay introduced by the ripple-carry process can become significant. To overcome this limitation, more advanced adder designs like carry-lookahead adders are used in high-performance systems.
2.3.5 Xor Xnor And Binary Adders
The Importance of XOR, XNOR, and Binary Adders
The humble XOR and XNOR gates might seem like simple building blocks, but their impact on modern computing is profound. They serve as the foundation of binary adders, which are essential for performing arithmetic operations on binary numbers. This ability is fundamental to the operation of modern computers, allowing them to execute complex algorithms, process information, and interact with the world around us.
By understanding the workings of XOR, XNOR, and binary adders, you’ve taken a crucial step into understanding the logical underpinnings of modern computing. You’ve learned about the building blocks of digital circuits and gained an appreciation for the elegant simplicity that drives the incredible complexity we see in today’s technologies. This knowledge can empower you to explore further and delve deeper into the fascinating world of digital logic and the innovation that continues to shape our future.





