Remember that time you were building a miniature model of a skyscraper with LEGOs? You might have meticulously measured everything, ensuring each brick was perfectly proportional to the real building. That, in essence, is the heart of what we’re exploring today – similar triangles. These fascinating geometric figures, with their harmonious ratios, play a pivotal role in understanding the world around us, from architecture to engineering to even the intricate patterns in nature. This comprehensive unit 6 study guide will unravel the mysteries of similar triangles, equipping you with the knowledge and skills to confidently navigate this exciting realm of geometry.

Image: jmrnfeafwc.blogspot.com
But why should you care about similar triangles? Imagine using them to calculate the height of a towering tree without climbing it or measuring the distance across a wide river without getting your feet wet. These are real-world applications of similar triangles, demonstrating their undeniable power and practical relevance. We’ll delve into these fascinating applications and explore the rich history behind these geometric wonders. Buckle up for an enriching journey through the world of similar triangles as we unlock their secrets, one concept at a time.
Understanding the Foundations: What are Similar Triangles?
Let’s kick things off by defining the stars of our show, similar triangles. Essentially, similar triangles are triangles that have the same shape but potentially different sizes. Imagine taking a photograph and then enlarging it; the image remains the same, but its size changes. This principle holds true for similar triangles – their corresponding angles are equal, and their corresponding sides are proportional. In simpler terms, if you have two triangles with the same angles, their sides are all in a fixed ratio.
The Cornerstones of Similarity: Key Properties
For two triangles to be considered similar, they must meet certain criteria. These criteria act as cornerstones, ensuring that the triangles share a fundamental geometric connection:
-
Equal Corresponding Angles: The most important condition! If all three corresponding angles of two triangles are equal, the triangles are similar. This property is crucial, as it guarantees the triangles share the same shape even if their sizes differ.
-
Proportional Corresponding Sides: The sides of similar triangles are in proportion – this implies that the ratios of the lengths of corresponding sides are equal. Imagine playing with a set of toy cars: each car is a proportional representation of a real car, showcasing the concept of proportionality within similar triangles.
Proving Similarity: Putting the Pieces Together
Now that we understand the key properties of similar triangles, let’s explore the different ways we can prove they are indeed similar. Each method serves as a powerful tool in the world of geometry:
-
Angle-Angle (AA) Postulate: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. This is the most commonly used method, as it allows us to quickly establish similarity based on angle measurements.
-
Side-Angle-Side (SAS) Similarity Theorem: If two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, then the triangles are similar. This theorem allows us to utilize both side lengths and angles to prove similarity, adding another dimension to our toolkit.
-
Side-Side-Side (SSS) Similarity Theorem: If three sides of one triangle are proportional to three sides of another triangle, then the triangles are similar. This theorem relies solely on side lengths and gives us a powerful way to conclusively determine if two triangles are similar – essentially comparing their side ratios.
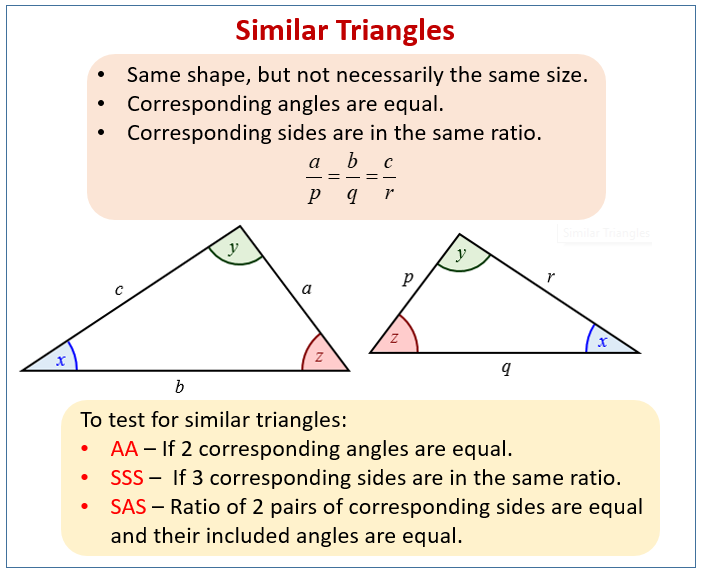
Image: www.onlinemathlearning.com
Real-World Applications: Similar Triangles in Action
Similar triangles aren’t just theoretical concepts confined to geometry textbooks; they play a crucial role in our everyday lives, from the buildings we live in to the technologies we use:
-
Architecture and Engineering: Similar triangles are essential in scaling models of buildings and bridges. Architects and engineers use them to ensure that proportions are maintained, guaranteeing structural integrity and safety. Imagine building a miniature model of a skyscraper using LEGOs; you’ll need to meticulously measure every brick to ensure it’s proportional to the real building, making use of similar triangle principles.
-
Surveying and Mapping: Similar triangles are vital in determining distances on land and at sea. Surveyors use them to measure distances that are otherwise impossible or impractical to access directly. For example, to find the distance across a wide river, surveyors can use similar triangles to create a small-scale version of the river and its surroundings, allowing them to calculate the actual distance.
-
Photography and Art: The principles of similar triangles are used in photography and art to create realistic perspectives and proportions. Artists use them to ensure that objects appear lifelike and to create the illusion of depth. Imagine tilting your camera lens to capture a panoramic view – your perspective changes, and the scene gets compressed, showcasing the subtle play of similar triangles in creating depth and dimension.
The Power of Ratios: Using Proportions to Solve Problems
A key concept intertwined with similar triangles is the use of ratios. Understanding ratios allows us to make connections between the corresponding sides of similar triangles, enabling us to solve for unknown lengths:
-
Calculating Unknown Side Lengths: Using the properties of similar triangles, we can establish proportions between the corresponding sides. By setting up these proportions, we can solve for unknown side lengths, even if those sides are difficult or impossible to measure directly. This ability to calculate unknown lengths has far-reaching implications in various fields, from architecture to engineering to even forensic investigations.
-
Understanding Scale Factors: Similar triangles are fundamentally about scale factors. The ratio of corresponding sides provides the scaling factor, indicating how much larger or smaller one triangle is compared to the other. This concept of scaling factors is crucial when dealing with maps, blueprints, or any situation where one object is a scaled representation of another.
Expert Tips and Strategies: Mastering the Art of Similar Triangles
Here are some expert tips to help you master the concepts and applications of similar triangles:
-
Practice, Practice, Practice: The key to mastering similar triangles is to practice solving problems. Use your textbook, online resources, or even create your own problems to get comfortable applying the concepts. The more you practice, the more confident you’ll become in your understanding of these powerful geometric principles.
-
Visualize and Annotate: Create diagrams and annotate them with key information, such as angles, side lengths, and proportions. Visualizing the relationships between triangles and their corresponding parts will aid in your understanding and problem-solving.
-
Look for Connections: Similar triangles are present in various situations. Pay attention to your surroundings and look for instances where similar triangles might be at play. This practice will help you develop an intuitive understanding of the concepts and their applications in the real world.
Unit 6 Study Guide Similar Triangles
Conclusion: Embracing the Power of Similar Triangles
Similar triangles are much more than just a chapter in your geometry textbook; they are fundamental building blocks of the world around us. By understanding their properties, their applications, and the various ways to prove their similarity, you’ll gain a deeper appreciation for the intricate beauty of geometry and its profound impact on our lives. So, don’t just learn about similar triangles – explore them, experiment with them, and unlock their secrets! The world of mathematics is waiting to be discovered, and similar triangles are your key to unlocking its wonders.





