Have you ever looked at a triangle and simply thought, “That’s just a triangle”? What if I told you there’s a whole world of hidden details and exciting classifications waiting to be discovered? It’s true! Triangles, those seemingly simple shapes we encounter everywhere from our homes to the natural world, are much more than just three-sided figures. Each triangle holds unique characteristics that help us understand its special properties and even solve complex mathematical problems. With a little exploration, we’ll unlock the secrets of classifying triangles, empowering you to see these shapes with new clarity and confidence.
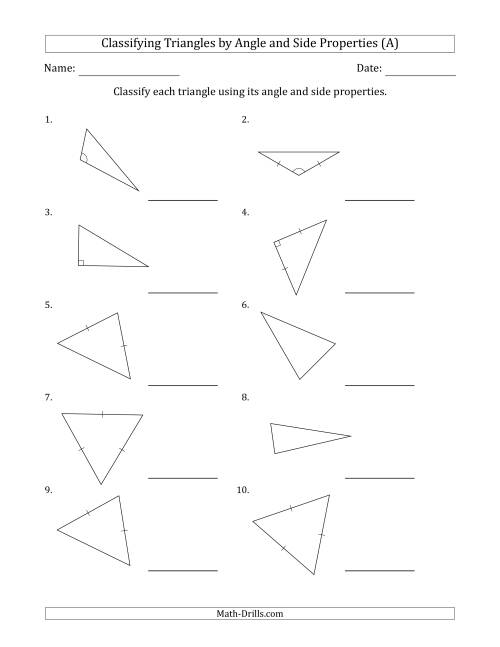
Image: www.math-drills.com
This journey into the world of triangles starts with a foundational understanding of their basic types. We’ll delve into the three main categories – scalene, isosceles, and equilateral – and explore how their angles and sides determine their overall classification. We’ll then move on to the concept of angle-based classification, uncovering the differences between acute, obtuse, and right triangles. By the end, you’ll understand not only how to define a triangle based on its shape and angles, but also how these classifications apply to real-world applications.
A Journey into the Triangle’s Inner World: Exploring Side Classifications
Imagine a triangle as a character in a story, each side revealing a vital piece of its personality. The first step in understanding these characters is by analyzing the lengths of their sides. Let’s break down the three main classifications based on side lengths:
1. Scalene Triangles: The Unique Individuals
Scalene triangles are the most “free-spirited” of the triangle family. Every side has a different length, making each scalene triangle unique. These triangles are often found in nature, where you can observe variations in the shapes of leafs, rocks, or even the constellations in the night sky.
- Distinctive Feature: All three sides have different lengths.
- Think of It As: A triangle that embraces its individuality, with no two sides the same.
- Real-World Examples: The pointed tip of a leaf, the uneven shape of a rock, or the constellation Orion.
2. Isosceles Triangles: The Balanced Partners
Isosceles triangles exude a sense of balance and symmetry. They have two sides of equal length and two angles of equal measure. These triangles can be found in everyday objects, like the roof of a house, the arms of a pair of scissors, or even the shape of a paperclip.
- Distinctive Feature: Two sides are equal in length, and two angles are equal in measure.
- Think of It As: A triangle that finds strength in balance.
- Real-World Examples: A house’s roof, the arms of a pair of scissors, a paperclip.
3. Equilateral Triangles: The Perfect Trio
Equilateral triangles are the epitome of perfection and harmony. They are known for their three equal sides and three equal angles, each measuring 60 degrees. These triangles are often seen in geometric art, natural patterns, and even the construction of strong and stable structures.
- Distinctive Feature: All three sides are equal in length, and all three angles are equal (60 degrees).
- Think of It As: A triangle that embodies perfect harmony and symmetry.
- Real-World Examples: A honeycomb, snowflakes, the face of a pyramid.
Diving Deeper: Angle Classifications
Now that we’re familiar with classifying triangles based on their sides, let’s explore how angles contribute to their unique character:
1. Acute Triangles: The Mighty Minis
Acute triangles are characterized by their three acute angles – each angle measuring less than 90 degrees. They are often described as “sharp” or “pointed” due to their smaller angles. They appear frequently in nature and architectural designs, showcasing a delicate balance between angles and sides.
- Distinctive Feature: All three angles are less than 90 degrees.
- Think of It As: A triangle that holds its strength in its sharp angles
- Real-World Examples: The triangular shapes in the corners of a room, the sail of a sailboat, the outline of a hummingbird’s wing.
2. Obtuse Triangles: The Bold and Brave
Obtuse triangles possess a single obtuse angle, which measures greater than 90 degrees, and two acute angles. They appear “rounded” due to their greater angle and often create a unique visual characteristic in designs and nature.
- Distinctive Feature: One angle is greater than 90 degrees.
- Think of It As: A triangle that commands attention with its bold angle.
- Real-World Examples: A tent, a slice of pizza, the wing of an aircraft.
3. Right Triangles: The Fundamental Foundation
Right triangles hold a special place in geometry, known for their one right angle (measuring exactly 90 degrees) and two acute angles. This unique combination of angles makes them crucial in understanding concepts like Pythagoras theorem, trigonometry, and the construction of various structures.
- Distinctive Feature: One angle is exactly 90 degrees.
- Think of It As: A triangle whose foundation rests on its right angle.
- Real-World Examples: Ladders leaning against walls, the diagonal of a square, the slope of a roof.
Applying Our Knowledge: Real-World Adventures
Classifying triangles isn’t just a theoretical exercise; it has real-life applications in fields like:
- Architecture: Architects use triangles to create stable and strong structures. The inherent rigidity of triangles, especially right triangles, makes them valuable in building bridges, towers, and other constructions.
- Engineering: Engineers rely on triangular principles in designing airplanes, automobiles, and other structures where stability and strength are crucial.
- Arts and Design: Artists and designers use triangles to create visual interest and balance in paintings, sculptures, and furniture designs. Triangles can evoke emotions, create rhythm, and enhance the overall aesthetic appeal of a work.
- Geometry and Mathematics: Mastering triangle classification is fundamental to understanding various mathematical concepts like Pythagoras theorem, trigonometry, and area and perimeter calculations.

Image: www.pinterest.com
Expert Tips for Mastering Triangle Classification
- Visualize: Draw triangles and label their sides and angles to help you visualize their properties.
- Real-World Examples: Look for triangles in and outside your environment. Observe how their side lengths and angles vary and how they contribute to the overall shape and stability of objects.
- Practice, practice, practice: The more you practice identifying triangles by their characteristics, the better you’ll become at recognizing them.
- Resources: Seek out online resources, tutorials, and games that focus on triangle classification to reinforce your learning.
Skills Practice Classifying Triangles 4 1
Concluding Thoughts: Embracing the World of Triangles
As you embark on your journey to understand the fascinating world of triangles, remember that classifying them is just the beginning. It’s a skill that will unlock a deeper understanding of geometry, mathematics, and the world around you. From the intricate patterns of nature to the sophisticated engineering designs that shape our lives, triangles hold endless potential for exploration and discovery. So, look closely at the next triangle you see, and remember, it might just hold a secret or two!





